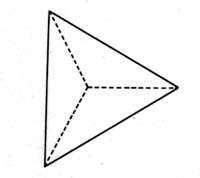
|
tetrahedron |
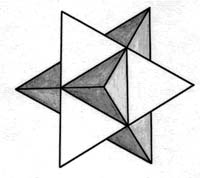
first stellation |
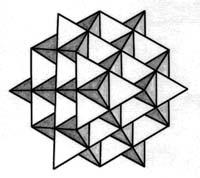
second stellation |
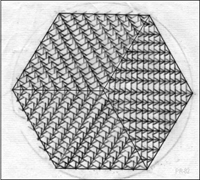
third stellation |
Approaching a Fractal Cube by
a series of non-convex polyhedra
 |
At the end of the 1970's, I came across Magnus J. Wenninger's beautiful book "Polyhedron Models" [1] where the author in an interesting way describes all the uniform polyhedra, some stellated forms and how to make colored paper models of them. That book instantly created the desire to make such models, and in the following years I much enjoyed making some of them...During that time I considered a "repetitive stellation procedure" to generate new polyhedra. The idea was to start with a Platonian solid, for example a tetrahedron, and then in a symmetric manner adding on its faces other tetrahedrons as shown in the four pictures above. In this way the first stellated form of the tetrahedron becomes Kepler's stella octangula. By (infinitely) repeating this process a series of non-convex polyhedra are generated (all made of identical equilateral triangles) which converge towards what may be called a "fractal cube", i.e., a solid with a fractal surface area. The Hausdorff dimension [2,3] of this fractal can be calculated to be 2.584963... (=ln6/ln2). |
|
|
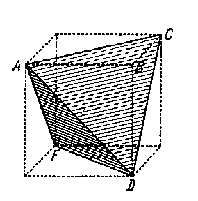
A tetrahedron inside a cube. The picture is a copy from Johannes Kepler's 'Harmonice Mundi', Book V, printed in 1619 [4]. The stellation process indicated above converges to the outer cube. The (infinite) sum of volumes for all tetrahedrons during the stellation process becomes equal to the volume of the outer cube. |
References[1] Magnus J. Wenninger. (1971). Polyhedron Models. London: Cambridge University Press. [2] Heinz G. Schuster. (1989). Deterministic Chaos. Second revised edition. Weinheim: VCH. [3] Heinz-Otto Peitgen, Hartmut Jürgens & Dietmar Saupe. (1992). Chaos and Fractals. New Frontiers of Science. New York: Springer-Verlag. [4] Johannes Kepler. (1978). Weltharmonik. Übersetzt und eingeleitet von Max Caspar. München: R. Oldenburg Verlag. |
|
|
